Analyse vectorielle

mardi 31 octobre 2006
par Laurent Marsal

En électromagnétisme, on manipule des fonctions vectorielles ou scalaires de la position d’un point M à l’instant t, appelés champs de vecteurs ou champs scalaires. Les lois physiques qu’ils décrivent font appel à une série de notions, en particulier la notion d’opérateur différentiel, que nous introduisons ici.
Plan de l’article :

I- Systèmes de coordonnées
II- Opérateurs différentiels
......2.1 Gradient
......2.2 Divergence
......2.3 Rotationnel
......2.4 Laplacien
......2.5 Nabla
III- Relations utiles entre opérateurs

I- Systèmes de coordonnées

On rappelle ici les 3 principaux types de coordonnées utilisées. $\vec{A}$ correspond à un champ de vecteurs.

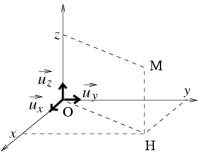
1.1 Coordonnées cartésiennes

base fixe $\left(\vec{u}_x ;\vec{u}_y ;\vec{u}_z\right)$
$\overrightarrow{OM}=x\vec{u}_x + y\vec{u}_y + z\vec{u}_z$
déplacement élémentaire : $d\overrightarrow{OM}=dx\vec{u}_x + dy\vec{u}_y + dz\vec{u}_z$
volume élémentaire : $d\tau=dx\cdot dy\cdot dz$
$\vec{A}=A_x\vec{u}_x + A_y\vec{u}_y + A_z\vec{u}_z$

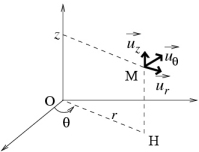
1.2 Coordonnées cylindriques

base mobile $\left(\vec{u}_r ;\vec{u}_{\theta} ;\vec{u}_z\right)$
$\overrightarrow{OM}=r\vec{u}_r + z\vec{u}_z$
déplacement élémentaire : $d\overrightarrow{OM}=dr\vec{u}_r + r\ d\theta\vec{u}_{\theta} + dz\vec{u}_z$
volume élémentaire : $d\tau=r\ dr\cdot d\theta\cdot dz$
$\vec{A}=A_r\vec{u}_r + A_{\theta}\vec{u}_{\theta} + A_z\vec{u}_z$

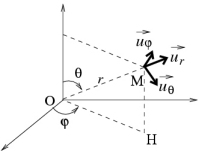
1.3 Coordonnées sphériques

base mobile $\left(\vec{u}_r ;\vec{u}_{\theta} ;\vec{u}_{\varphi}\right)$
$\overrightarrow{OM}=r\vec{u}_r$
déplacement élémentaire : $d\overrightarrow{OM} = dr\vec{u}_r + rd\theta\vec{u}_{\theta} + r\sin\theta d\varphi\vec{u}_{\varphi}$
volume élémentaire : $d\tau=r^2\sin\theta dr\cdot d\theta\cdot d\varphi$
$\vec{A}=A_r\vec{u}_r + A_{\theta}\vec{u}_{\theta} + A_{\varphi}\vec{u}_{\varphi}$

II- Opérateurs différentiels

Les opérateurs différentiels sont des combinaisons de dérivées partielles par rapport aux coordonnées d’espace.

2.1 Gradient
2.1.1 Définition et propriétés

Le gradient s’applique à un champ scalaire $f$ et renvoie un champ vectoriel.

Définition : soit $f$ un champ scalaire, de variation élémentaire $df$ pour un déplacement élémentaire du point $M$ . Le gradient du champ scalaire $f$ est le champ vectoriel $\overrightarrow{\textrm{grad}}\ f$ tel que :

$df = \overrightarrow{\textrm{grad}}\ f\cdot d\overrightarrow{OM}$

Propriété 1 : en tout point $M$ , $\overrightarrow{\textrm{grad}}\ f$ est un vecteur orthogonal à la surface équi- $f$ passant par $M$ .

Propriété 2 : en tout point $M$ , $\overrightarrow{\textrm{grad}}\ f$ est dirigé vers les $f$ croissants.

Propriété 3 : la circulation d’un gradient est indépendante du chemin suivi : $\int_A^B\overrightarrow{\textrm{grad}}\ f\cdot d\overrightarrow{OM} =\int_A^B df=f(B)-f(A)$ .
Par conséquent, la circulation d’un gradient sur un contour fermé est nulle.

2.1.2 Expressions

-Coordonnées cartésiennes :

$\overrightarrow{\textrm{grad}}\ f = \frac{\partial f}{\partial x}\vec{u}_x + \frac{\partial f}{\partial y}\vec{u}_y + \frac{\partial f}{\partial z}\vec{u}_z$

-Coordonnées cylindriques :

$\overrightarrow{\textrm{grad}}\ f = \frac{\partial f}{\partial r}\vec{u}_r + \frac{1}{r}\frac{\partial f}{\partial \theta}\vec{u}_{\theta} + \frac{\partial f}{\partial z}\vec{u}_z$

-Coordonnées sphériques :

$\overrightarrow{\textrm{grad}}\ f = \frac{\partial f}{\partial r}\vec{u}_r + \frac{1}{r}\frac{\partial f}{\partial \theta}\vec{u}_{\theta} + \frac{1}{r\sin\theta}\frac{\partial f}{\partial \varphi}\vec{u}_{\varphi}$

2.2 Divergence
2.2.1 Définition et propriétés

La divergence s’applique à un champ vectoriel $\vec{A}$ et renvoie un champ scalaire.

Définition : soit $\vec{A}$ un champ vectoriel, soit $d\tau$ un volume élémentaire entourant le point $M$ , et soit $dS$ la surface élémentaire limitant $d\tau$ . Soit enfin $d\Phi$ le flux élémentaire sortant du champ $\vec{A}$ à travers la surface $dS$ . On appelle divergence en $M$ du champ $\vec{A}$ le champ scalaire $\textrm{div}\ \vec{A}$ tel que :

$d\Phi = \textrm{div}\ \vec{A}\cdot d\tau$

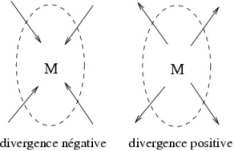
Propriété 1 : la divergence d’un champ caractérise dans quelle proportion ce champ diverge en un point de l’espace.

Propriété 2 : (théorème de Green-Ostrogradski) soit $S$ une surface fermée, orientée vers l’extérieur, et limitant un volume $V$ . Le flux sortant de $\vec{A}$ à travers $S$ est égal à l’intégrale de volume de $\textrm{div}\ \vec{A}$ sur le volume $V$ .

$\int\hspace*{-0.28cm}\int_S\hspace*{-0.56cm}\bigcirc\ \vec{A}\cdot\vec{n}\ dS = \int\hspace*{-0.28cm}\int\hspace*{-0.28cm}\int_V \textrm{div}\ \vec{A}\cdot d\tau$

Propriété 3 : un champ $\vec{A}$ est à flux conservatif si $\textrm{div}\ \vec{A}=0$ . Son flux à travers toute surface fermée est nul. Son flux est le même à travers toutes les surfaces appuyées sur le même contour.

2.2.2 Expressions

-Coordonnées cartésiennes :

$\textrm{div}\ \vec{A} = \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z}$

-Coordonnées cylindriques :

$\textrm{div}\ \vec{A} = \frac{1}{r}\frac{\partial (rA_r)}{\partial r} + \frac{1}{r}\frac{\partial A_{\theta}}{\partial \theta} + \frac{\partial A_z}{\partial z}$

-Coordonnées sphériques :

$\textrm{div}\ \vec{A} = \frac{1}{r^2}\frac{\partial (r^2A_r)}{\partial r} + \frac{1}{r\sin\theta}\frac{\partial (\sin\theta A_{\theta})}{\partial \theta} + \frac{1}{r\sin\theta}\frac{\partial A_{\varphi}}{\partial \varphi}$

2.3 Rotationnel
2.3.1 Définition et propriétés

Le rotationnel s’applique à un champ vectoriel $\vec{A}$ et renvoie un champ vectoriel.

Définition : soit $\vec{A}$ un champ vectoriel, soit $d\Gamma$ un contour élémentaire, fermé et orienté, entourant le point $M$ , et soit $dS$ la surface élémentaire limitée par $d\Gamma$ . Soit enfin $dC$ la circulation élémentaire du champ $\vec{A}$ sur le contour orienté $d\Gamma$ . On appelle rotationnel en $M$ du champ $\vec{A}$ le champ vectoriel $\overrightarrow{\textrm{rot}}\ \vec{A}$ tel que :

$dC = \overrightarrow{\textrm{rot}}\ \vec{A}\cdot\vec{n}\ dS$

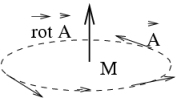
Propriété 1 : le rotationnel d’un champ permet d’exprimer comment, localement en un point $M$ , le champ $\vec{A}$ tourne autour de $M$ .

Propriété 2 : (théorème de Stokes-Ampère) soit $\Gamma$ un contour fermé, limitant une surface (ouverte) $S$ orientée d’après $\Gamma$ . La circulation de $\vec{A}$ sur le contour orienté $\Gamma$ est égale au flux sortant de $\overrightarrow{\textrm{rot}}\ \vec{A}$ à travers $S$ .

$\oint_{\Gamma} \vec{A}\cdot\overrightarrow{dl} = \int\hspace*{-0.28cm}\int_S \overrightarrow{\textrm{rot}}\ \vec{A}\cdot\vec{n}\ dS$

Propriété 3 : un champ $\vec{A}$ dérive d’un potentiel si $\overrightarrow{\textrm{rot}}\ \vec{A}=\vec{0}$ . Sa circulation sur un contour fermé est nulle. Sa circulation sur un circuit quelconque ne dépend que des extrémités du circuit.

2.3.2 Expressions

-Coordonnées cartésiennes :

$\overrightarrow{\textrm{rot}}\ \vec{A} = \left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}\right)\vec{u}_x + \left(\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}\right)\vec{u}_y + \left(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)\vec{u}_z$

-Coordonnées cylindriques :

$\overrightarrow{\textrm{rot}}\ \vec{A} = \left(\frac{1}{r}\frac{\partial A_z}{\partial \theta}-\frac{\partial A_\theta}{\partial z}\right)\vec{u}_r + \left(\frac{\partial A_r}{\partial z}-\frac{\partial A_z}{\partial r}\right)\vec{u}_{\theta} + \frac{1}{r}\left(\frac{\partial (rA_{\theta})}{\partial r}-\frac{\partial A_r}{\partial \theta}\right)\vec{u}_z$

-Coordonnées sphériques :

$\overrightarrow{\textrm{rot}}\ \vec{A} = \frac{1}{r\sin\theta}\left(\frac{\partial (A_{\varphi}\sin\theta)}{\partial \theta}-\frac{\partial A_\theta}{\partial \varphi}\right)\vec{u}_r + \frac{1}{r}\left(\frac{1}{\sin\theta}\frac{\partial A_r}{\partial \varphi}-\frac{\partial (rA_{\varphi})}{\partial r}\right)\vec{u}_{\theta} + \frac{1}{r}\left(\frac{\partial (rA_{\theta})}{\partial r}-\frac{\partial A_r}{\partial \theta}\right)\vec{u}_{\varphi}$

2.4 Laplacien
2.4.1 Laplacien scalaire

Il s’applique à un champ scalaire $f$ et renvoie un champ scalaire.

Définition : $\Delta f = \textrm{div}\ \left(\overrightarrow{\textrm{grad}}\ f\right)$

Expressions :
-Coordonnées cartésiennes :

$\Delta f = \frac{\partial^2f}{\partial x^2} + \frac{\partial^2f}{\partial y^2} + \frac{\partial^2f}{\partial z^2}$

-Coordonnées cylindriques :

$\Delta f = \frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial f}{\partial r}\right) + \frac{1}{r^2}\frac{\partial^2f}{\partial\theta^2} + \frac{\partial^2f}{\partial z^2}$

-Coordonnées sphériques :

$\Delta f=\frac{1}{r}\frac{\partial^2(rf)}{\partial r^2} + \frac{1}{r^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial f}{\partial\theta}\right) + \frac{1}{r^2\sin^2\theta}\frac{\partial^2f}{\partial \varphi^2}$

On notera en particulier que $\Delta(1/r)=0$ en coordonnées sphériques.

2.4.2 Laplacien vectoriel

Il s’applique à un champ vectoriel $\vec{A}$ et renvoie un champ vectoriel.

Définition : $\Delta \vec{A} = \overrightarrow{\textrm{grad}}\ \left(\textrm{div}\ \vec{A}\right) - \overrightarrow{\textrm{rot}}\ \left(\overrightarrow{\textrm{rot}}\ \vec{A}\right)$

Expression en coordonnées cartésiennes :

$\Delta \vec{A} = \Delta A_x\vec{u}_x + \Delta A_y\vec{u}_y + \Delta A_z\vec{u}_z$

2.5 Opérateur nabla

C’est un vecteur symbolique, noté $\vec{\nabla}$ , qui permet de noter commodément les différents opérateurs différentiels :

$\overrightarrow{\textrm{rot}}\ \vec{A}=\vec{\nabla}\wedge\vec{A}$

$\textrm{div}\ \vec{A}=\vec{\nabla}\cdot\vec{A}$

$\overrightarrow{\textrm{grad}}\ f=\vec{\nabla} f$

$\Delta f = \vec{\nabla}^2 f$

Notons en particulier qu’en coordonnées cartésiennes, on a :

$\vec{\nabla} = \frac{\partial}{\partial x}\vec{u}_x + \frac{\partial}{\partial y}\vec{u}_y + \frac{\partial}{\partial z}\vec{u}_z$

III- Relations utiles entre opérateurs

Tous les opérateurs différentiels sont linéaires. On a les relations suivantes :

$\textrm{div}\ \left(\overrightarrow{\textrm{rot}}\ \vec{A}\right) = 0$

$\textrm{div}\ \left(f\vec{A}\right) = f\cdot\textrm{div}\ \vec{A} + \vec{A}\cdot\overrightarrow{\textrm{grad}}\ f$

$\textrm{div}\ \left(\vec{A}\wedge\vec{B}\right) = \vec{B}\cdot\overrightarrow{\textrm{rot}}\ \vec{A} - \vec{A}\cdot\overrightarrow{\textrm{rot}}\ \vec{B}$

$\overrightarrow{\textrm{rot}}\ \left(\overrightarrow{\textrm{grad}}\ f\right) = \vec{0}$

$\overrightarrow{\textrm{rot}}\ \left(f\vec{A}\right) = f\cdot\overrightarrow{\textrm{rot}}\ \vec{A} - \vec{A}\wedge\overrightarrow{\textrm{grad}}\ f$

$\overrightarrow{\textrm{rot}}\ \left(\overrightarrow{\textrm{rot}}\ \vec{A}\right) = \overrightarrow{\textrm{grad}}\ \left(\textrm{div}\ \vec{A}\right) - \Delta\vec{A}$

$\overrightarrow{\textrm{grad}}\ (f\cdot g) = f\cdot\overrightarrow{\textrm{grad}}\ g + g\cdot\overrightarrow{\textrm{grad}}\ f$

$\Delta(f\cdot g) = f\cdot\Delta g + 2\ \grad f\cdot\grad g + g\cdot\Delta f$

$\oint_{\Gamma} f\cdot\overrightarrow{dl} = - \int\hspace*{-0.28cm}\int_S\overrightarrow{\textrm{grad}}\ f\wedge \overrightarrow{dS}$

$\int\hspace*{-0.28cm}\int_S\hspace*{-0.56cm}\bigcirc\ f\cdot\overrightarrow{dS} = \int\hspace*{-0.28cm}\int\hspace*{-0.28cm}\int_V\overrightarrow{\textrm{grad}}\ f\cdot d\tau$

$\int\hspace*{-0.28cm}\int_S\hspace*{-0.55cm}\bigcirc\ \vec{B}\wedge\overrightarrow{dS} = - \int\hspace*{-0.28cm}\int\hspace*{-0.28cm}\int_V\overrightarrow{\textrm{rot}}\ \vec{B}\cdot d\tau$

Analyse vectorielle

I- Systèmes de coordonnées

1.1 Coordonnées cartésiennes

1.2 Coordonnées cylindriques

1.3 Coordonnées sphériques

II- Opérateurs différentiels

2.1 Gradient

2.1.1 Définition et propriétés

2.1.2 Expressions

2.2 Divergence

2.2.1 Définition et propriétés

2.2.2 Expressions

2.3 Rotationnel

2.3.1 Définition et propriétés

2.3.2 Expressions

2.4 Laplacien

2.4.1 Laplacien scalaire

2.4.2 Laplacien vectoriel

2.5 Opérateur nabla

III- Relations utiles entre opérateurs

Publications

Derniers articles publiés

Statistiques

Dernière mise à jour

Publication

Visites

Navigation

Articles de la rubrique

Brèves

Présentations prépas

Quelques liens CPGE